
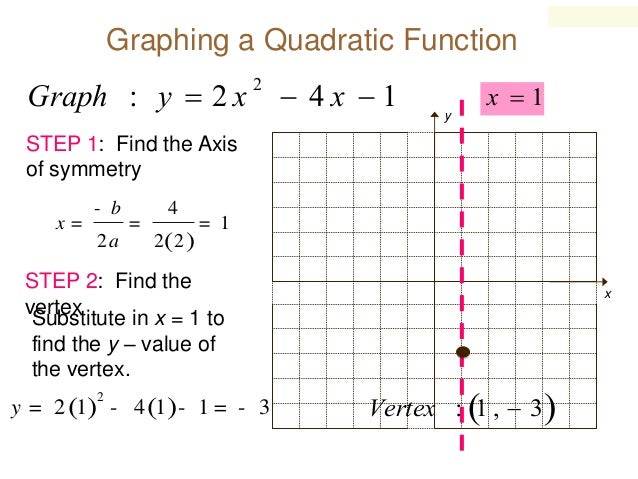

Exercises for Graphing Quadratic Functions Graphing Quadratic Functions in Standard Form Sketch the graph of each function. Now, you can simply graph the quadratic function. Substitute zero for \(x\) and solve for \(y\). Graphing Quadratic Functions – Example 2: Graphing Quadratic Functions in Standard Form Graphing Quadratic Functions – Example 1:įirst, recall that a Quadratic function in vertex form is \(y=a(x – h)^2+k\) where \((h,k)\) is the vertex of the function. To graph a quadratic function, first find the vertex, then substitute some values for \(x\) and solve for \(y\).Quadratic functions in standard form: \(y=ax^2+bx+c\) where \(x=-\frac\) is the value of \(x\) in the vertex of the function.Quadratic functions in vertex form: \(y=a(x – h)^2+k\) where \((h,k)\) is the vertex of the function.Step by step guide to Graphing Quadratic Functions + Ratio, Proportion and Percentages Puzzles.
#QUADRATIC FUNCTION GRAPH FREE#
+ ISEE Middle-Level Math Worksheets: FREE & Printable.+ 3rd Grade Mathematics Worksheets: FREE & Printable.+ FTCE General Knowledge Math Worksheets.We can plot the graph of a quadratic function by drawing a table of values for the x x and y y coordinates, and then plotting these on a set of axes. Let us see how this discriminant b 2 - 4ac can be used to know the nature of the roots of a quadratic function. What are quadratic graphs Quadratic graphs are graphs of quadratic functions that is, any function which has x2 x2 as its highest power. The discriminant b 2 - 4ac discriminates the nature of the zeros of the quadratic function f(x) = ax 2 + bx + c. Otherwise, the parabola will be open downward.Ģ4. To know at where the parabola cuts y-axis or y-intercept of the parabola, we have to plug x = 0 in the given quadratic function.Ģ3. f(x) = ax 2 + bx + c, if the sign of the first term ( ax 2 ) is negative, the parabola will be open downward. If the vertex and a point on the parabola are known, apply vertex form. If the x-intercepts are known from the graph, apply intercept form to find the quadratic function. x- coordinate of the vertex of the parabola is -b/2a and the vertex is (-b/2a, f(-b/2a)).Ģ2. Write the Quadratic Functions This set of printable worksheets requires high school students to write the quadratic function using the information provided in the graph. The two x-intercepts of a parabola (graph of a quadratic function) are nothing but the zeros of the quadratic function.Ģ1. If the two zeros of a quadratic function are imaginary, then the graph (parabola) will never intersect x - axis.Ģ0. The zeros of a quadratic equation are the x-coordinates of the points where the parabola (graph of quadratic a function) cuts x-axis.ġ9. The graph of any quadratic function will be a parabola.ġ8. If one root is equal to other root but opposite in sign then their sum = 0. If one zero is reciprocal to the other root then their product c/a = 1 or c = a.ġ6. The product of the zeros of the quadratic function f(x) = ax 2 + bx + c is c/a.ġ5. The sum of the zeros of the quadratic function f(x) = ax 2 + bx + c is -b/a.ġ4. That is, if (m + √n)is a root, then (m - √n) is the other root of the same equation.ġ3. If the two zeros of a quadratic function are irrational, then the two zeros (roots) will occur in conjugate pairs. There are three methods to find the two zeros (x-intercepts) of a quadratic function. If the graph of a quadratic function opens up and the vertex is below the x-axis or if the graph opens down and the vertex is above the x-axis, then there will be two x-intercepts.ġ1. The x-axis or if the graph opens down and the vertex is below the x-axis,ĩ. If the vertex is touching the x-axis, then there is one x-intercept regardless of whether the graph opens up or down.ġ0. The number of x-intercepts of a quadratic function depends on whether the graph opens up or down and it also depends on whether the vertex is above or below the x-axis.Ĩ. If the graph of a quadratic function opens up and the vertex is above The zeros of a quadratic function f(x) = ax 2 + bx + c are the two x-intercepts of the parabola.ħ. The zeros of a quadratic function f(x) = ax 2 + bx + c are the two values of x when f(x) = 0 or ax 2 + bx + c = 0.Ħ. (ii) if a < 0 (parabola opens down), the range is (-∞, k].ĥ. In f(x) = a(x - h) 2 + k, if a > 0, the parabola opens up and if a 0 (parabola opens up), the range is [k,∞). The vertex form of a quadratic function isģ. The graph of a quadratic function is a parabola.Ģ. The domain of a quadratic function f(x) = ax 2 + bx + c is all real numbers.


 0 kommentar(er)
0 kommentar(er)
